浮点数在计算机中的存储方式
整数在计算机中的表示方式为补码,可以做到在取值范围中的一一对应,即精确的表示范围内的每个整数。而浮点数想要做到一一对应是不可能的,毕竟内存资源有限。不过浮点数的表示范围在相同的字节数下却能比整数多很多,这是为何呢?
References:
- http://steve.hollasch.net/cgindex/coding/ieeefloat.html
- http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html
- http://www.cnblogs.com/jillzhang/archive/2007/06/24/793901.html
由于浮点数不能一一对应,所以不能用和整数一样的存储文式,根据IEEE标准,使用科学计数法来编码数字,基数和指数。例如,123.456可以表示为1.23456×10^2。十六进制数123.abc可能表示为1.23abc×16^2.在二进制中,数字10100.110可以表示为1.0100110×2^4。
IEEE浮点数具有三个基本组成部分:符号(sign),指数(exponent)和尾数(mantissa)。尾数由小数和隐含的前导数字组成。指数基(2)是隐式的,不需要存储。
按照位排列,浮点数字如下所示:
单精度:SEEEEEEE EMMMMMMM MMMMMMMM MMMMMMMM
双精度:SEEEEEEE EEEEMMMM MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM
- 符号位
存储在第一个二进制位,只占一位。就如同它的名字一样,表示数字的符号。0表示正数,1表示负数。改变该位的值会改变数字的符号。 - 指数
单精度占8位,双精度占11位。指数也有正负指数,为了避免过多的符号位,所以指数部分不再单独分出一位表示符号,而是为其添加一个偏移量。以单精度为例,即实际值为0~256对应指数的-127~128。因此对于IEEE单精度浮点数,该偏移值为127。指数为零意味着127存储在指数部分中。存储值200表示(200-127)即73的指数。-127(全0)和+128(全1)的指数被保留用于特殊数字,原因稍后讨论。
对于双精度,指数字段为11位,偏移量为1023。 - 尾数
单精度占23位,双精度占52位。尾数,也被称为有效数,代表数字的精度。它由一个隐含的前导位(小数点的左侧)和小数位(在小数点的右侧)组成。
为了找出隐含的前导位的值,可以考虑以多种不同的方式用科学符号来表示任何数字。例如,50可以表示为以下任何一个:
.5000×10^2
0.050×10^3
5000.×10^-2
为了最大化可表示数量的数量,浮点数通常以规范化形式存储,将小数点放在第一个非零数字之后。在规范化形式中,5表示为5.000×10^0。
在规范形式的基础上,我们可以使用一个不错的小优化,因为二进制下只有一个可能的非零数字:1。因此,我们只能假设1为前导数字,因此也不需要将其存储在浮点表示中。所以,32位浮点值具有24位尾数:23个显式的小数位加一个隐式前导位(1)。
总结一下:
- 符号位正值为0,负数为1。
- 指数基数为2。
- 指数字段存储值为127加上单精度的真实指数,或1023加上双精度的真实指数。
- 尾数的第一位通常假定为1.f,其中f是小数位。
关于浮点数的表示范围本文不再介绍,需要了解的可查看参考链接或自行查阅资料。
特殊值
IEEE保留指数部分为全0和全1的值,以表示浮点方案中的特殊值。
- 零(Zero)
如上所述, 由于假定了前导数1,所以零不能被直接表示。零是用指数和尾数都是全零表示的一个特殊值. 注意−0和+0是不同的值, 虽然在大小比较上是一样的。 - 非规范化(Denormalized)
如果指数全为0,但小数为非零(否则将被解释为零),则该值为非规范化数,此时的前导值为0。因此,这样表示一个数字(-1)^s×0.f×2^-126,其中s是符号位,f是小数。对于双精度,非规范化数字为(-1)^s×0.f×2^-1022。从这来说可以将零解释为特殊类型的非规范化数字。
随着非规范化数字越来越小,它们逐渐失去精度,因为分数的左位变为零。在规范值为24位的情况下,最小非规范化值(只有最低有效小数位为1),32位浮点数只有一位精度。 - 无穷(Infinity)
+∞和-∞用指数全1和小数全0来表示。符号位区分负无穷大和正无穷大。将无穷大表示为特定值是有用的,这允许在数据溢出的情况下继续操作。对无穷值的操作在IEEE浮点数中被很好地定义(这部分请阅读第一个参考链接)。 - 非数字(Not A Number)
值NaN(非数字)用于表示不是实数的值。NaN由指数全1和非零的小数部分表示。有两种类型的NaN:QNaN(Quiet NaN)和SNaN(Signalling NaN)。
QNaN小数部分最高位为1。QNaN通过大多数算术运算自由地传播。当一个操作的结果不是数学上定义的时候,这些值就产生了。
SNaN小数部分最高位为0。它用于在操作中使用时发出异常信号。SNaN可以方便地分配给未初始化的变量来捕获过早使用的异常。
语义上,QNaN表示不确定的操作,而SNaN表示非法操作。
下面来实际的看下
定义浮点数1.5,由内存地址中得到存储的数据为3fc00000,来分析下这个数: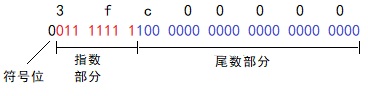
将其转为二进制后如上图所示。
即1.1*2^(127-127)。
啊~这篇写的好累啊~~!
 这破站
这破站