判断一个数是否为2的幂
写代码无意中看到java.util.Random中的nextInt(int bound)方法, 有这么两行代码让我虎躯一震。
int m = bound - 1;
if ((bound & m) == 0) // i.e., bound is a power of 2这就能检测一个数是不是2的幂了???
References:
- https://stackoverflow.com/questions/600293/how-to-check-if-a-number-is-a-power-of-2
- https://blog.csdn.net/c5113620/article/details/79065696
- 《Hacker’s Delight》by Henry S. Warren
看到上面代码后不能理解,于是查了下,这就是所谓的奇技淫巧吧。由于二进制的特性:
- 2的n次方的二进制只有最高位是1,其余为0
- -1后最高位向后借位为0,其余为1
利用这个特性将 (给定数) 和 (给定数 - 1) 按位做"与"操作后,如果是2的幂会发现,所有bit都是0。
这里以一个byte长度的数为例,忽略第一位符号位,第二位为1,其余为0时的数为64,将其-1后得到63,高位1变为0,其余位变为1。64和63按位与后就变成0了。
所以利用这个方式可以很高效的判断一个数是否为2的幂,如下所示
static boolean isPowerOfTwo(long x) {
return (x & (x - 1)) == 0;
}这段代码还有点缺陷,对于特殊值0,这段代码也返回true,但0并不是2的幂。所以完善代码如下:
static boolean isPowerOfTwo(long x) {
return (x & (x - 1)) == 0 && (x > 0);
}我在看到这段惊为天人的代码后想,以前的大佬是真大佬,把二进制特性都利用的这么充分。然后在一篇文章中看到了《Hacker’s Delight》的字样,就去书里找了下,发现了宝藏: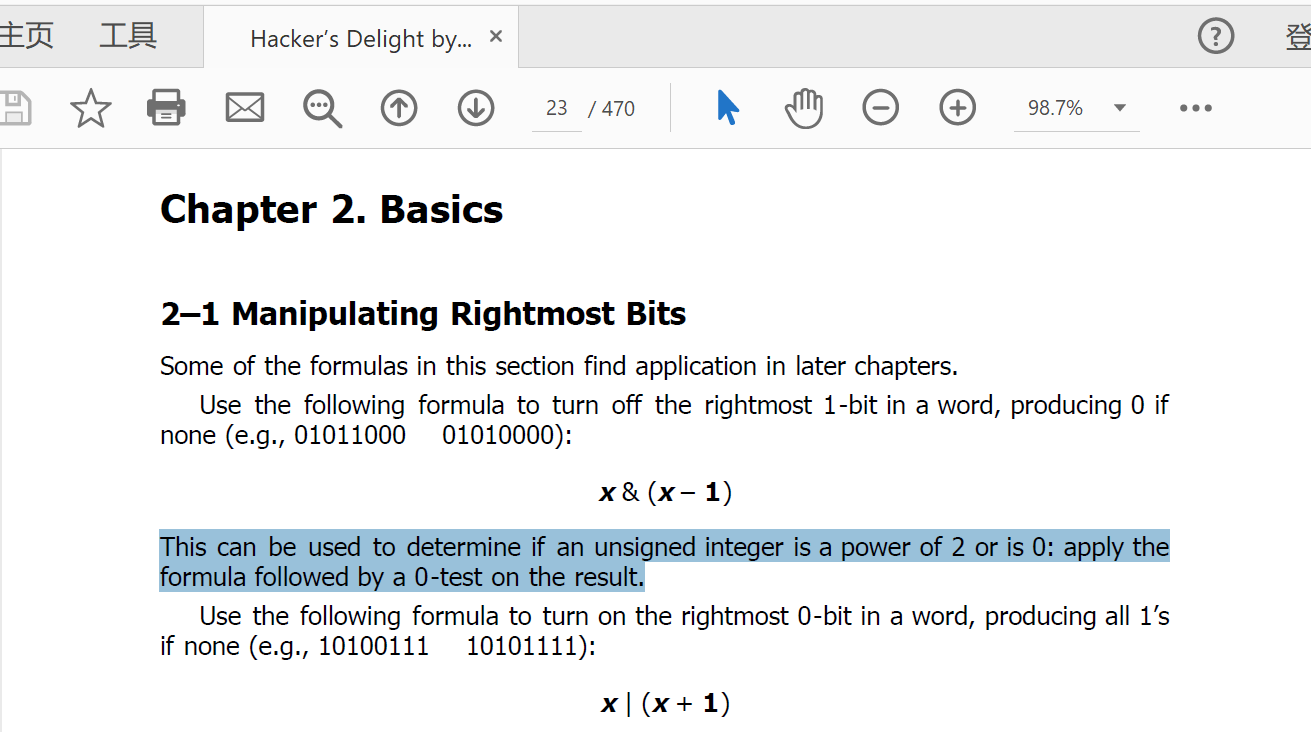
书的第二章第一节就是教各种位操作的,第一个就是上文说的检测2的幂,而且是轻描淡写的带过。可惜后面全是各种运算,完全看不懂,不然真想好好看看这本书,哈哈,还是先找些看得懂的吧,慢慢来。
 这破站
这破站
秒懂 赞了